Definisi Getaran Harmonik
Getaran harmonik diartikan sebagai gerak dari sebuah benda dimana grafik posisi partikel berperan sebagai fungsi waktu berupa sinus, artinya dapat dinyatakan dalam bentuk sinus maupun kosinus. Gerak ini disebut dengan getaran harmonik atau gerak osilasi.
Contoh Getaran Harmonik dalam Kehidupan Nyata
Berikut merupakan beberapa contoh dari getaran harmonik yang sering ditemui.
- Gelombang radio.
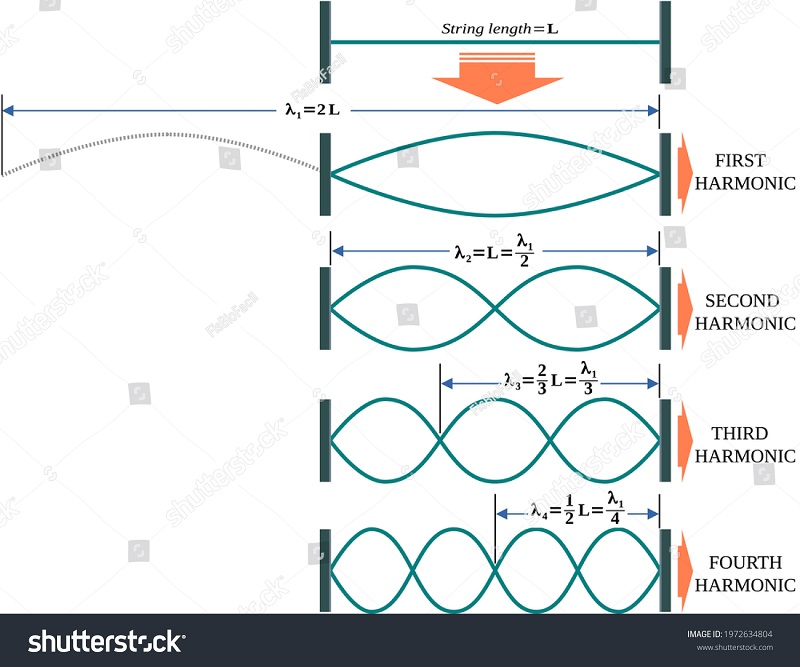
- Dawai pada alat musik.
- Denyut jantung.
- Arus listrik AC.
Syarat Terjadinya Getaran Harmonik
Terdapat beberapa syarat yang harus dipenuhi hingga suatu gerak dapat dikatakan sebagai getaran harmonik, diantaranya adalah:
- Gerakannya selalu melampau posisi keseimbangan.
- Memiliki gerakan bolak-balik (periodik).
- Gaya atau arah percepatan yang bekerja pada sebuah benda akan selalu mengarah pada posisi keseimbangan.
- Gaya atau percepatan yang bekerja pada suatu benda sebanding dengan simpangan atau posisi benda.
Frekuensi dan Periode Getaran Harmonik
a. Frekuensi dan Periode Sistem Pegas
Secara garis besar, gerak harmonik merujuk pada suatu gerak melinkar beraturan di salah satu sumbu utamanya. Oleh karena itu, frekuensi dan periode pada pegas dapat dikalkulasikan dengan menyamakan gaya pemulih (F = -kX) dan gaya sentripetal (F = -4π 2 mf2X). Diketahui, frekuensi dan periode dari sebuah sistem beban pegas bergantung pada konstanta dan massa gaya pegas itu sendiri.
b. Frekuensi dan Periode Bandul Sederhana
Suatu bandul sederhana terdiri dari beban bermassa m yang digantung pada ujung tali ringan, dengan massa yang dapat diabaikan, memiliki panjang l. Jika beban ditarik ke satu sisi kemudian dilepaskan, beban tersebut akan berayun melalui titik keseimbangan ke arah yang berlawanan.
Apabila amplitudo kecil, bandul akan melakukan getaran harmonik. Sehingga bisa disimpulkan, frekuensi dan periode getaran pada bandul sederhana hampir sama seperti pegas. Dalam hal ini, frekuensi dan periodenya bisa dihitung dengan menyamakan gaya sentripetal dan gaya pemulih.
Gaya Yang Bekerja Pada Bandul Sederhana
Persamaan gaya pemulih dari bandul sederhana bisa digambarkan dengan F = -mg sinθ. Dimana untuk sudut θ kecil, dicatat dalam satuan radian, maka sinθ = θ . Oleh sebab itu, persamaannya berubah menjadi F = -mg (X/l). Mengingat persamaan gaya sentripetal ialah F = -4π 2 mf2X, maka dapati diperoleh persamaan sebagai berikut.
Frekuensi dan periode bandul sederhana tidak bergantung pada simpangan bandul maupun massa, melainkan hanya bergantung pada percepatan gravitasi setempat dan panjang tali.
Contoh Soal Getaran Harmonik
Agar lebih jelas, berikut merupakan rincian rumus beserta contoh soal dari getaran harmonik.
y = 0,04 sin 20π t
Dengan asumsi y adalah simpangan dalam satuan meter dan t adalah waktu dalam satuan sekon, tentukan beberapa besaran yang tercipta dari persamaan getaran harmonik tersebut.
- Amplitudo
- Frekuensi
- Periode
- Simpangan Maksimum
- Simpangan pada saat t = 1/60 sekon
- Simpangan pada saat sudut fasenya 45 derajat
- Sudut fase pada saat simpangannya 0,02 meter
Pembahasan soal
Berdasarkan soal di atas, akan didapat pola persamaan simpangan gerak harmonik sebagai berikut.
y = A sin ωt
ω = 2π f
atau
ω = 2π/T
- Amplitudo
y = 0,04 sin 20π t
A = 0,04 meter
- Frekuensi
y = 0,04 sin 20π t
ω = 20π
2πf = 20π
f = 10 Hz
- Periode
T = 1/f
T = 1/10 = 0,1 s
- Simpangan Maksimum
y = A sin ωt
y = ymaks sin ωt
y = 0,04 sin 20π t
y = ymaks sin ωt
ymaks = 0,04 m
- Simpangan pada saat t = 1/60 sekon
y = 0,04 sin 20π t
y = 0,04 sin 20π (1/60)
y = 0,04 sin 1/3 π
y = 0,04 sin 60° = 0,04 × 1/2√3 = 0,02 √3 m
- Simpangan pada saat sudut fasenya 45 derajat
y = A sin ωt
y = A sin θ
Dengan asumsi θ adalah sudut fase, θ = ωt
y = 0,04 sin θ
y = 0,04 sin 45° = 0,04 (0,5√2) = 0,02√2 m
- Sudut fase pada saat simpangannya 0,02 meter
y = 0,04 sin 20π t
y = 0,04 sin θ
0,02 = 0,04 sin θ
sin θ = 1/2
θ = 30°
Itulah sekilas informasi mengenai definisi getaran harmonik lengkap dengan syarat, rumus beserta contoh soalnya.